摘要
我们都知道二叉查找树的查找的时间复杂度是O(log N),其查找效率已经足够高了,那为什么还有B树和B+树的出现呢?难道它两的时间复杂度比二叉查找树还小吗?
答案当然不是,B树和B+树的出现是因为另外一个问题,那就是磁盘IO;众所周知,IO操作的效率很低,那么,当在大量数据存储中,查询时我们不能一下子将所有数据加载到内存中,只能逐一加载磁盘页,每个磁盘页对应树的节点。造成大量磁盘IO操作(最坏情况下为树的高度)。平衡二叉树由于树深度过大而造成磁盘IO读写过于频繁,进而导致效率低下。
所以,我们为了减少磁盘IO的次数,就你必须降低树的深度,将“瘦高”的树变得“矮胖”。一个基本的思路就是:
- 每个节点存储多个元素
- 摒弃二叉树结构,采用多叉树
这样就引出来了一个新的查找树结构 ——多路查找树。 根据AVL给我们的启发,一颗平衡多路查找树(B~树)自然可以使得数据的查找效率保证在O(log N)这样的对数级别上。
B树
定义
首先得了解什么是B树的阶:
所有节点度的最大值(孩子节点数)为B树的阶。
m阶B树的特性
- 每个节点最多有m棵子树(该节点有m-1个关键字)
- 根节点若非终端节点(叶子节点),则至少有2棵子树,不受[m/2]向上取整的约束
- 除根节点外的所有非叶子节点至少有[m/2]向上取整棵子树,[m/2]-1向上取整个关键字
- 所有叶子节点都出现在同一层上,并不带任何信息
关键字数 树高 [m/2]-1 <= n <= m-1 logm(n+1) <= h <= log[m/2](n+1)/2+1 B树的结构
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15template<class Record,int order>//order表示B树的阶
struct node{
int count;//节点中关键字的个数
Record data[order-1];//阶数-1个关键字
node<Record,order>* branch[order];//分支表
node();
}
template<class Record,int order>
class btree{
private:
node<Record,order>* root;//树根
public:
...
}
查找
1 | template<class Record,int order> |
B树的插入
定位
利用B树的查找,找到最底层中的某个非叶子节点
插入
注意关键字个数在[m/2]-1 ~ m-1内,否则进行节点分裂
例如3阶B树分裂,关键字数范围[1,2],中间节点上移,以该节点分裂:

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32template<class Record,int order>
bool insert(const Record &new_entry){
Record median;//分裂后的中间元素
node<Record,order>* right_branch,*new_root;
bool result = push_down(root,new_entry,right_branch);
if(result==overflow){
new_root = new node<Record,order>;
new_root->count=1;
new_root->data[0]=median;
new_root->branch[0]=root;
new_root->branch[1]=right_branch;
root = new_root;
}
return 1;
}
template<class Record,int order>
push_down(node<Record,order>* current,
const Record &new_entry,
node<Record,order>* &right_branch){
int posi;
if(current==null){
median = new_entry;
right_branch=null;
result = overflow;
}else{
if(search(current,new_entry,posi))
result = duplicate_error;
else
Record 未完待续。。。
}
}
B树的删除
删除终端节点
- 节点关键字数 > [m/2]-1,直接删除
- 节点关键字数 = [m/2]-1
- 兄弟够借,通过父亲借兄弟
- 兄弟不够借,拉父下水一起穷
删除非终端节点(找前驱/后继取代法)
找到取代关键字后与法1相同。
总结
- B树主要用于文件系统以及部分数据库索引,例如:
MongoDB。而大部分关系数据库则使用B+树做索引,例如:mysql数据库; - 从查找效率考虑一般要求B树的阶数m >= 3;
- B-树上算法的执行时间主要由读、写磁盘的次数来决定,故一次I/O操作应读写尽可能多的信息。因此B-树的结点规模一般以一个磁盘页为单位。一个结点包含的关键字及其孩子个数取决于磁盘页的大小。
B+树
B+树是B树的变种,有着比B树更高的查询效率。下面,我们就来看看B+树和B树有什么不同
特征
一个关键字对应一个分支,即n个关键字的节点有n棵子树(B树中是k-1个关键字对应k棵子树),每个元素不保存数据,只用来索引,所有数据都保存在叶子节点。
所有的叶子结点中包含了全部元素的信息,及指向含这些元素记录的指针,且叶子结点本身依关键字的大小
自小而大顺序链接。非叶子节点中的关键字为对应子树的最大关键字(非叶子节点仅起到索引的作用)。
下面是一棵3阶的B+树:
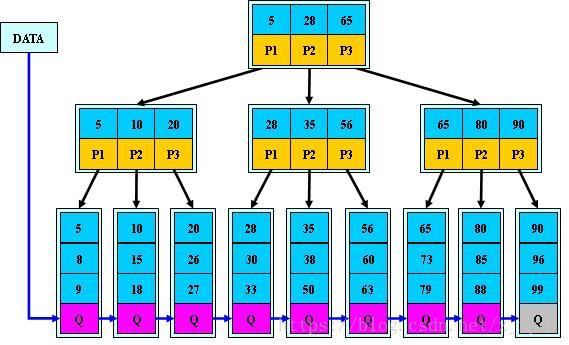
B+树通常有两个指针,一个指向根结点,另一个指向关键字最小的叶子结点。因些,对于B+树进行查找两种运算:一种是从最小关键字起顺序查找,另一种是从根结点开始,进行随机查找。
查找
B+树的优势在于查找效率上,下面我们做一具体说明:
首先,B+树的查找和B树一样,类似于二叉查找树。起始于根节点,自顶向下遍历树,选择其分离值在要查找值的任意一边的子指针。在节点内部典型的使用是二分查找来确定这个位置。
(1)、不同的是,B+树中间节点没有卫星数据(索引元素所指向的数据记录),只有索引,而B树每个结点中的每个关键字都有卫星数据;这就意味着同样的大小的磁盘页可以容纳更多节点元素,在相同的数据量下,B+树更加“矮胖”,IO操作更少
B树的索引数据:
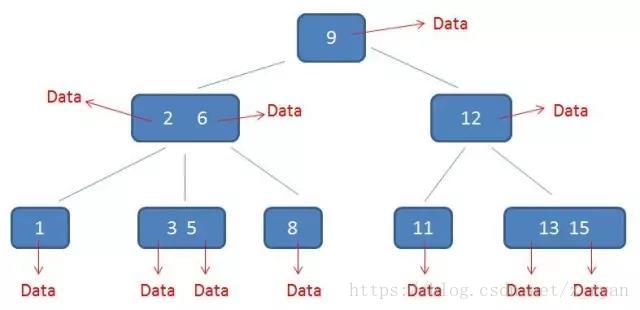
B+树的索引数据:
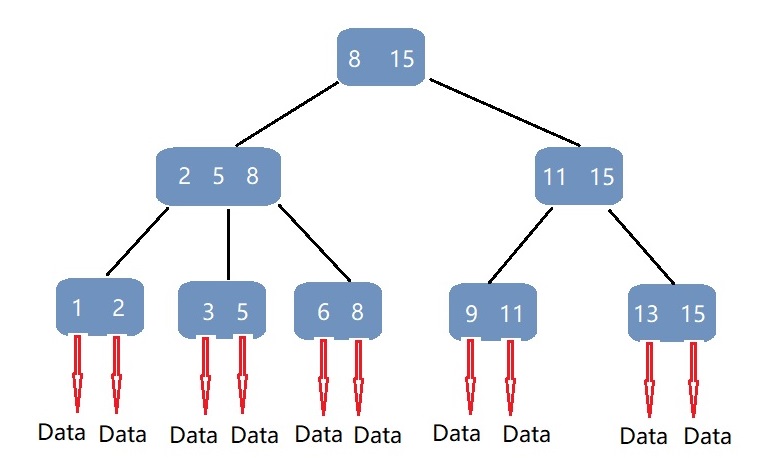
在数据库的聚集索引(Clustered Index)中,叶子节点直接包含索引数据。在非聚集索引(NonClustered Index)中,叶子节点带有指向索引数据的指针。
其次,因为索引数据的不同,导致查询过程也不同;B树的查找只需找到匹配元素即可,最好情况下查找到根节点,最坏情况下查找到叶子结点,所说性能很不稳定,而B+树每次必须查找到叶子结点,性能稳定
在范围查询方面,B+树的优势更加明显
- B树的范围查找需要不断依赖中序遍历。首先二分查找到范围下限,在不断通过中序遍历,知道查找到范围的上限即可。整个过程比较耗时。
- 而B+树的范围查找则简单了许多。首先通过二分查找,找到范围下限,然后同过叶子结点的链表顺序遍历,直至找到上限即可,整个过程简单许多,效率也比较高。
例如:同样查找范围[3-11],两者的查询过程如下:
- B树的查找过程:
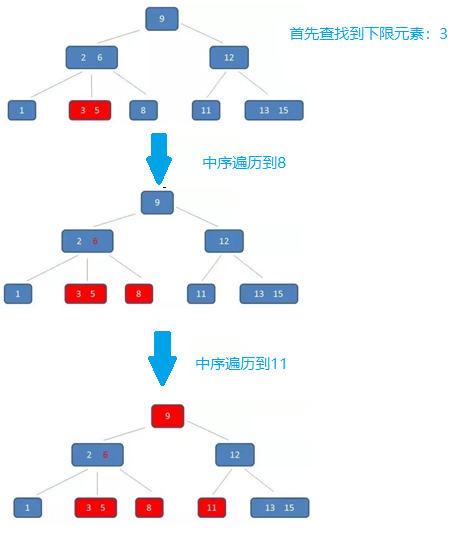
- B+树的查找过程:
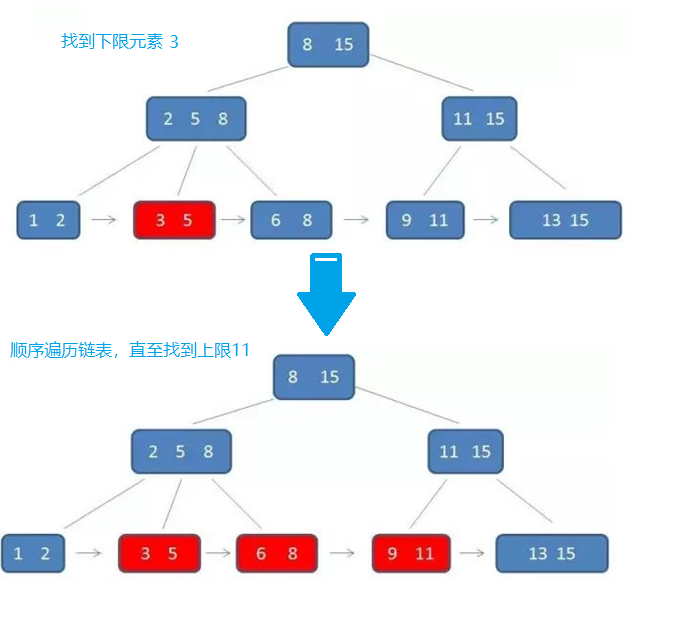
插入
B+树的插入与B树的插入过程类似。不同的是B+树在叶结点上进行,如果叶结点中的关键码个数超过m,就必须分裂成关键码数目大致相同的两个结点,并保证上层结点中有这两个结点的最大关键码。
删除
B+树中的关键码在叶结点层删除后,其在上层的复本可以保留,作为一个”分解关键码”存在,如果因为删除而造成结点中关键码数小于ceil(m/2),其处理过程与B-树的处理一样。在此,我就不多做介绍了。
总结
B+树相比B树的优势:
- 单一节点存储更多的元素,使得查询的IO次数更少;
- 所有查询都要查找到叶子节点,查询性能稳定;
- 所有叶子节点形成有序链表,便于范围查询。

